Fastai Lesson 3
Deep Learning from Scratch
Disclaimer:
In the unlikely event that the person reading this is not me, please make sure to check out the actual course “Deep Learning for Coders” over at course.fast.ai. These summaries are written with an audience of one - me - in mind, so proceed with caution.
Building a neural network from scratch
In line with the top-down nature of the course, the first two installments of this series (Lesson 1, Lesson 2) dealt with the use of the high-level API to train and apply pre-trained models. This section covers the inner workings of deep learning models and fundamental elements of the training process, namely stochastic gradient descent (SGD).
As such, this part of the course is the most crucial building block for understanding the more sophisticated methodologies introduced later on.
To provide a practical application for this lesson, we will use the MNIST dataset as a sandbox for our model. For now, however, we will try to make the problem as simple as possible. As such we will not go for recognizing all ten possible digits but focus only on a small subset at first. The goal will be to build some system from scratch which can successfully differentiate between zeros and ones.
The MNIST dataset
We will be working with the famous MNIST dataset (Deng, 2012), which is a collection of images depicting handwritten digits. Is is a widely used dataset for image classification tasks. As such it is also available for download from kaggle.com, which is where I obtained the files for this exercise. A straighforward approach to fetching data from Kaggle is to install the Kaggle API and execute the following in your chosen directory:
kaggle competitions download -c digit-recognizer
This will provide you with the following files:
sample_submission.csv
test.csv
train.csv
The dataset is provided as a training and a test set, conveniently prepared to directly work with. But before we dive into modelling, let’s take a look at the contents of the provided files. To do that, I will load the data into a pandas DataFrame, split it into a training and validation set, and take a look at the first few rows:
train_df = pd.read_csv('train.csv')
valid_df = train_df.sample(axis=0, frac=0.2, random_state=1337)
train_df = train_df.drop(valid_df.index)
train_df = train_df.reset_index(drop=True)
valid_df = valid_df.reset_index(drop=True)
train_df.head()
| label | pixel0 | pixel1 | pixel2 | pixel3 | pixel4 | pixel5 | pixel6 | pixel7 | pixel8 | ... | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
5 rows × 785 columns
As you can see in the table, data in train.csv is structured in a way that every row represents one image. Accordingy, the first column provides the label of the digit we are trying to find and the remaining 784 rows each represent one pixel of the 28x28 image.
This is an important insight to appreciate. Even if we are working with an image recognition problem, the underlying data is nothing more than a collection of pixel values. This becomes even more evident when we dive deeper into the data. So let’s go on to achieve the next milestone in our data preperation - PyTorch tensors for the independent and dependent variables of our model. Remember that we restricted our problem to only ones and zeros, which is why we will start by filtering the dataset for those two labels and then prepare the tensors.
train_ones = []
train_zeros = []
for i in train_df.index:
if train_df.iloc[i]['label'] == 1:
train_ones.append(tensor(train_df.iloc[i, 1:].values).reshape((28, 28)))
elif train_df.iloc[i]['label'] == 0:
train_zeros.append(tensor(train_df.iloc[i, 1:].values).reshape((28, 28)))
train_ones = torch.stack(train_ones).float()/255
train_zeros = troch.stack(train_zeros).float()/255
So now we have a stacked tensor of size 3764x28x28 of pixel values for all ones and zeros in the MNIST dataset. To make it more clear, what we each element represents, let’s plot one of them:
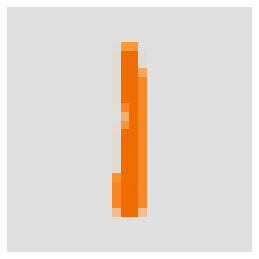
This singular one is a beautiful specimen of what we want our model to find. It also shows how pixel values in our data relate to images. While this is a rather straightforward thought, it is an important point to grasp - we should always be aware of what the numbers in our model actually represent.
So how to we approach the task of building a neural net from scratch? As Jeremy Howard proposes, we will start with a simple and intuitive baseline.
A simple baseline
Before worrying about how to build a neural network, let’s try to think of a way to solve the problem by other means. So how would we be able to differentiate between zeros and ones? One approach would be to figure out, what an “average” zero/ one looks like and compare each digit to that mean value.
Let’s take a look at what those idealized digits would look like:
mean1 = train_ones.mean(0)
mean0 = train_zeros.mean(0)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 5), sharey=True)
show_image(mean1, ax=ax[0], cmap=orange_palette, figsize=(5,5))
show_image(mean0, ax=ax[1], cmap=orange_palette, figsize=(5,5))
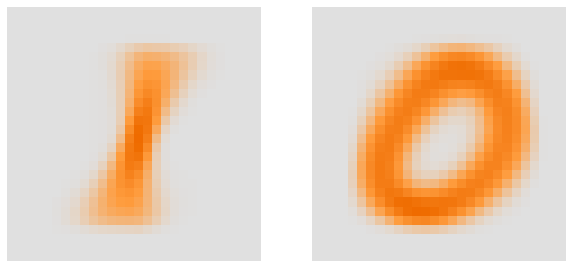
Having established what we expect a one or zero to look like, we can compare a given one
(a_1 = train_ones[0]). In order to do that we will need to calculate the difference between our
input and the average. This is where the loss function comes in which we have covered in the
previous lessons. We will start with two commonly used loss functions:
Mean Absolute Error (MAE) - a.k.a. L1 Loss
Root Mean Squared Error (RMSE) - a.k.a. L2 Loss
Don’t worry about the math. It becomes much simpler once it is written out as code. So let’s compare our example one to each of our two averages:
(a_1 - mean1).abs().mean()
(a_1 - mean0).abs().mean()
This provides is with a value for the loss compared to each digit:
(tensor(0.0845), tensor(0.1933))
It looks like the calculated loss is lower for mean1 than for mean0. This is already a good
sign. By the way, PyTorch provides us with a function for L1 Loss already, so we would have
achieved the same result by calling F.l1_loss(a_1, mean1) - F is the recommended name to import
torch.nn.functional.
Similarly, RMSE becomes much more straightforward when viewed as code:
((a_1 - mean1)**2).mean().sqrt()
((a_1 - mean0)**2).mean().sqrt()
(tensor(0.2080), tensor(0.3263))
Again, we can use PyTorch for this: F.mse_loss(a_1, mean1).sqrt()
To apply this to our validation set, we will turn it into a python function and pass all ones to
it:
def mnist_distance(a, b):
return (a - b).abs().mean((-1, -2)) # we only want to include the axes with pixel values
valid_ones_dist = mnist_distance(valid_ones, mean1)
valid_ones_dist.shape
torch.Size([920])
This returns a list of 920 loss values, then number of ones we have in our validation set.
Equipped with a loss function, we can define our prediction function based on the comparison which yields the lower loss:
def is_one(x):
return mnist_distance(x, mean1) < mnist_distance(x, mean0)
So, in order to figure out whether whether the image contains a zero or a one, we can simply pass it to our new prediction function:
is_one(a_1)
tensor(True)
This seems to work well based on single example. But in order to verify how well our model works, we need some performance metric (as covered in the previous lessons). For our examples, we will use accuracy as our metric, by counting the number of correctly classified digits:
accuracy_ones = is_one(valid_ones).float().mean()
accuracy_zeros = (1 - is_one(valid_zeros).float()).mean()
accuracy_ones, accuracy_zeros
(tensor(1.), tensor(0.8810))
Who would have thought? It looks like our model can already predict ones with 100% accuracy and zeros with an accuracy of 88%! The problem is only, that our model has no way of improving. What this approach is currently lacking is the key process underlying deep learning - stochastic gradient descent.
Sochastic Gradient Descent
In order to build a process that learns from our loss function, we will need some sort of weight assignment. So, instead of comparing against some mean or “ideal” representation of each digit, we calculate weights that are highest for the most important pixels for a particular digit. Accordingly, we could think of the probability of an image being a one as the sum of each pixel multiplied by some weight:
def prob_1(x, w):
"""Calculate the probability of the image being a one, given pixels and weights."""
return (w * x).sum()
The problem now is to find the right weights so that a high probability is returned for real ones. We need to figure out an approach of updating these weights to make them incrementally better at predicting ones. This process is stochastic gradient descent.
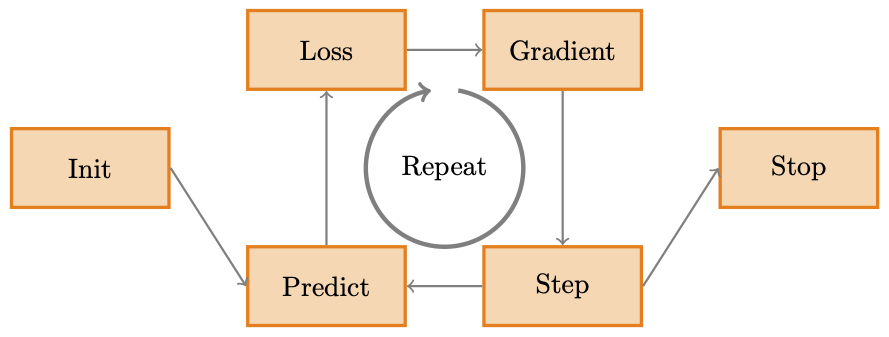
As the image above shows, it works its magic using only a few simple steps:
- Initialize a set of parameters randomly
- Predict the label of each image using these parameters
- Calculate the Loss of the model based on these predictions
- Calculate the gradient to calculate the impact of changing parameters on loss
- Step (i.e. change) all weights slightly in the direction of the lower loss
- Repeat steps 2 though 5
- Stop the training process
So in order to apply this to our problem, we need to turn our images into a dataset. Generally
speaking, a PyTorch dataset is expected to by structured in such a way, that it returns a tuple of
(x, y). To achieve this, we will first combine all of our images (x) into a single stacked
tensor:
train_x = torch.cat([train_ones, train_zeros]).view(-1, 28*28)
train_x.shape
torch.Size([7039, 784])
Next, we need to create a tensor with our labels, i.e. the actual digit we are trying to predict. To
do so, we simply insert a 1 for every entry in train_ones and a 0 for each entry in
train_zeros:
train_y = tensor([1] * len(train_ones) + [0] * len(train_zeros)).unsqueeze(1)
train_y.shape
torch.Size([7039, 1])
Finally, to turn these two tensors into the expected list of tuples, we can simply use zip:
dset = list(zip(train_x, train_y))
x, y = dset[0]
x.shape, y
(torch.Size([784]), tensor([1]))
We need to repeat these steps, accordingly, to create our validation set. Once this is done, we can go through the seven steps of the gradient descent process in turn:
Initialize
In order to initialize parameters, we define a simple function that returns random numbers based on a provided shape:
def init_params(size, std=1.0):
"""Randomly intiialize parameters based on a standard deviation."""
return (torch.randn(size)*std).requires_grad_()
We use this to initialize one parameter for each pixel in our 28x28 images and another number as the bias.
weights = init_params((28*28, 1))
bias = init_params(1)
Predict
Having randomly initialized the parameters of our model. We will use them to predict the digit of an
image. We could to this simply by calculating (train_x[0]*weights.T).sum() + bias. In order to be
able to pass an entire batch of data, however, we will use matrix multiplication. This is what our
prediction function now looks like:
def linear1(xb):
"""Calculate the prediction for a set of images."""
return xb @ weights + bias
Accordingly, we can now simply pass the entire dataset:
preds = linear1(train_x)
preds
tensor([[ 1.7234],
[-1.2711],
[-4.2819],
...,
[ 2.2772],
[-4.0504],
[ 5.0252]], grad_fn=<AddBackward0>)
Loss
Now that we can predict the digit depicted in an image based on our parameters, we can use those
predictions to calculate the model’s loss. Since there are only two labels, 0 and 1, we can
define a very simple loss function, i.e. we simply compute the difference between the actual label
and the prediction:
def mnist_loss(predictions , targets):
predictions = predictions.sigmoid() # we use the sigmoid function to ensure predictions are between 0 and 1
return torch.where(targets==1, 1-predictions, predictions).mean()
The below example illustrates how this works:
trgts = tensor([1, 0, 1])
preds = tensor([0.9, 0.4, 0.2])
loss = mnist_loss(preds, trgts)
loss
tensor(0.4460)
Gradient
The loss shows model how far off the current set of parameters is. In order to improve our
parameters, we need to calculate the gradient for each of them. PyTorch makes it incredibly
straightforward to calculate the gradient, given we have defined our parameters with
requires_grad_() and as floating point numbers. Below is an example with the first three entries
of our training dataset:
weights = init_params((28*28, 1))
bias = init_params(1)
trgts = tensor(train_y[3])
preds = linear1(tensor(train_x[3]))
loss = mnist_loss(preds, trgts)
loss.backward()
weights.grad.shape, weights.grad.mean(), bias.grad
(torch.Size([784, 1]), tensor(-0.0052), tensor([-0.1160]))
Step
With our gradients in hand, we can use them to change our parameters in the direction of lower loss.
The size of the step is called the learning rate (lr):
lr = 1e-5
weights.data -= lr * weights.grad.data
Repeat
Now that we can calculate the losses and gradients and we can use them to optimize the parameters, we can create the actual training loop. First, however, there is another important element to think about. How many elements should we use to calculate the loss? We could take the entire training set, but that would be to computationally expensive. We could also just take a single item, but that would only give us enough information to optimize for this specific image. The compromize is then to split the training set into mini-batches and calculate the loss based on these subsets.
Hint: A larger batch size leads to a more accurate and stable estimate but will take longer
PyTorch provides the DataLoader class for this. It is basically a generator, yielding one batch of
the dataset at a time:
data = range(15)
dl = DataLoader(data, batch_size=5, shuffle=True)
list(dl)
[tensor([ 0, 7, 14, 4, 13]),
tensor([10, 9, 6, 3, 8]),
tensor([11, 5, 12, 2, 1])]
A generic training loop would then look something like this:
for x, y in dl:
pred = model(x)
loss = loss_pred(pred,y)
loss.backward()
parameters -= parameters.grad * lr
To implement this in our dataset, we will do the following:
- Create our DataLoader
- Create a function to repeat the previous steps
- Build a training loop similar to the one above
- Define a function to calculate the accuracy of the model
- Build a validation loop
# Create our DataLoader
dl = DataLoader(dset, batch_size=256)
valid_dl = DataLoader(valid_dset, batch_size=256)
# Create a function to calculate the prediction and loss
def calc_grad(xb, yb, model):
preds = model(xb)
loss = mnist_loss(preds, yb)
loss.backward()
# Define training loop
def train_epoch(model, lr, params):
for xb, yb in dl:
calc_grad(xb, yb, model)
for p in params:
p.data -= p.grad * lr
p.grad.zero_() # this resets the gradients after our step
# Measure accuracy
def batch_accuracy(xb, yb):
preds = xb.sigmoid()
correct = (preds > 0.5) == yb
return correct.float().mean()
# Validation loop
def validate_epoch(model):
accs = [batch_accuracy(model(xb), yb) for xb, yb in valid_dl]
return round(torch.stack(accs).mean().item(), 4)
So let’s try measuring the accuracy and see whether it improves after training for one epoch:
validate_epoch(linear1)
0.3181
lr = 1.
params = weights, bias
train_epoch(linear1, lr, params)
validate_epoch(linear1)
0.8471
It works! Let’s see what happens if we train for a few more epochs:
for i in range(5):
train_epoch(linear1, lr, params)
print(validate_epoch(linear1), end='\n')
0.9673
0.9836
0.9904
0.9921
0.9927
So now we have a simple training loop which allows us to find zeros and ones with an impressive accuracy.
Using PyTorch and fastai
PyTorch and fastai provide helpful simplifications for the above steps. Firstly, our function
linear1 is already implemented as nn.Linear and can be initialized by providing the input and
output dimenions:
linear_model = nn.Linear(28*28, 1)
w, b = linear_model.parameters()
w.shape, b.shape
(torch.Size([1, 784]), torch.Size([1]))
Secondly, fastai provides the handy learner class which takes virtually all of the effort out of
creating a training process. For instance, the implementation of stochastic gradient descent we have
been working on so far, can simply be added to the class as SGD:
learn = Learner(dls, nn.Linear(28*28, 1), opt_func=SGD, loss_func=mnist_loss, metrics=batch_accuracy)
learn.fit(5, lr=lr)
| epoch | train_loss | valid_loss | batch_accuracy | time |
|---|---|---|---|---|
| 0 | 0.169611 | 0.029667 | 0.997749 | 00:00 |
| 1 | 0.068044 | 0.009250 | 0.997749 | 00:00 |
| 2 | 0.035621 | 0.005843 | 0.998312 | 00:00 |
| 3 | 0.020956 | 0.004643 | 0.998312 | 00:00 |
| 4 | 0.013350 | 0.003998 | 0.998312 | 00:00 |
Building a Neural Net
So far, our function is limited, in that it is only a linear function. To move to a neural network, we need to add a non-linear element between two linear functions. That is basically the entire definition of a neural net - two linear classifiers with a max function between them:
def simple_net(xb):
res = xb @ w1 + b1
res = res.max(tensor(0.0)) # identical to F.relu
res = xb @ w2 + b2
return res
Just like before, w1, b1, w2, b2 are randomnly initialized parameters:
w1 = init_params((28*28, 30))
b1 = init_params(30)
w2 = init_params((30, 1))
b2 = init_params(1)
Note that 30 is randomly chosen. It means here that w1 has 30 output activations and can therefore
construct 30 different features, i.e. different constellations of pixels. w2 accordingly, needs to
have the same number of input activations. Increasing this number makes the model more capable to
model complex functions.
The very simple relu function adds as an if statement and thereby decouples layers to remove
linearity.
The lines of code in the simple_net are referred to as layers. In this case, two linear
layers with a nonlinearity, or activation function.
Just as before, PyTorch provides a simple implementation of this already:
simple_net = nn.Sequential(nn.Linear(28*28, 30),
nn.ReLU(),
nn.Linear(30, 1))
nn.Sequential creates a module that will call each of the listed layers in turn and we can use it
just like our original model.
learn = Learner(dls, simple_net, opt_func=SGD, loss_func=mnist_loss, metrics=batch_accuracy)
learn.fit(5, 0.1)
This is theoretically everything that is needed to solve any complex function - SGD and a single nonlinearity with two linear layers. Anything that comes from here is optimization!
What is our network actually learning?
I have mentioned the paper of Matthew D. Zeiler and R. Fergus before (Zeiler & Fergus, 2014) in a previous post. In it, the authors provide a fascinating insight into how a convolutional neural network learns to recognize increasingly complex visual features throughout its layers. Let’s see what our simple neural net is learning about recognizing ones.
To do so, we will simply extract the parameters of our first linear layer and plot them as a 28x28 pixel image:
m = learn.model
w, b = m[0].parameters() # the parameters of the first linear layer
w[0].view(28, 28)
show_image(w[3].view(28, 28), figsize=(5,5), cmap=full_palette)
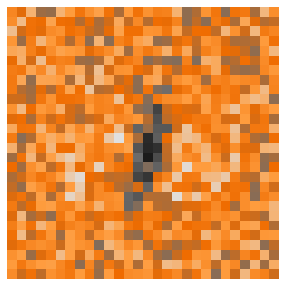
It looks like this set of weights is optimized for finding a vertical bar in the center of the image, typical for the digit one. Isn’t this fascinating?
One more thing: Moving to Multi-Class Classification
The chapter in the book (Howard & Gugger, 2020) ends with a homework assignment, asking the reader to apply these principles to the entire MNIST dataset.
So far, we have only built a classifier to distinguish between zeros and ones, i.e. binary classification. To solve the MNIST problem, however, we need to be able to classify all 10 handwritten digits.
Let’s start by preparing out data for the full set just as before:
# Turn the pixel values of the DataFrames into tensors:
train_x = tensor(train_df.iloc[:,1:]).float()/255
train_y = tensor(train_df.iloc[:,0])
valid_x = tensor(valid_df.iloc[:,1:]).float()/255
valid_y = tensor(valid_df.iloc[:,0])
# Combine the independent and dependent variables into a dataset:
dset = list(zip(train_x, train_y))
valid_dset = list(zip(valid_x, valid_y))
# Create a DataLoader for training and validation:
dl = DataLoader(dset, batch_size=5, shuffle=True)
valid_dl = DataLoader(dset, batch_size=5)
# Combine both into a single DataLoaders instance:
dls = DataLoaders(dl, valid_dl)
dls.one_batch()
(tensor([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]),
tensor([7, 2, 1, 8, 7]))
So as you can see, this looks just like before, just that we now have more than two possible labels.
The first key change we need to make is to the architecture of the model. Our simple_net returned
a single number for each set of pixels and was able to provide the probability of the input being a
one. If we want to account for 10 numbers, we need to increase the output dimension to 10
accordingly:
mnist_net = nn.Sequential(nn.Linear(28*28, 30),
nn.ReLU(),
nn.Linear(30, 10))
The second key change we need to make to our learner is the loss function so as to be able to deal
with more than one class. Remember our mnist_loss function used sigmoid to turn activations into
numbers between zero and one, denoting the probability of each of the two classes. Therefore, we
were able to calculate the loss by computing the difference to the actual number.
In this case, this will not work, because our dependent variable takes more shapes than just zero and one.
Let’s start with the same learner we used before and taking a look at the activations our loss function will see:
x, y = dls.one_batch()
preds,_ = learn.get_preds(dl=[(x, y)])
preds[0]
tensor([ 0.0820, 0.0791, -0.2281, -0.1365, -0.2006, 0.0334, -0.2755, -0.0951,
-0.0061, -0.0384])
len(preds[0]), preds[0].sum()
(10, tensor(-0.7858))
As you can see, these probabilities do not add up to one, as they did before. Similar to what we did
with the sigmoid function in mnist_loss, we want to turn our activations into numbers between zero
and one, adding up to 100%. But rather than the probability of finding a one and its inverse, we
want to achieve this for 10 numbers.
Softmax achieves this:
Let’s look at the impact on our data:
sm_acts = torch.softmax(preds, dim=1)
sm_acts
tensor([[0.1165, 0.1162, 0.0855, 0.0937, 0.0879, 0.1110, 0.0815, 0.0976, 0.1067,
0.1033],
[0.1219, 0.1070, 0.0861, 0.0888, 0.0924, 0.1109, 0.1011, 0.0850, 0.1033,
0.1034],
[0.1157, 0.1120, 0.0830, 0.0971, 0.0995, 0.1103, 0.0911, 0.1046, 0.0996,
0.0871],
[0.1152, 0.1115, 0.0910, 0.0909, 0.0924, 0.1042, 0.0918, 0.0926, 0.1071,
0.1034],
[0.1192, 0.1122, 0.0928, 0.1003, 0.0917, 0.1072, 0.0849, 0.0889, 0.1001,
0.1027]])
len(sm_acts[0]), sm_acts[0].sum()
(10, tensor(1.0000))
Now all that is left to do is adapt the learner, accordingly, and train!
learn = Learner(dls, mnist_net, opt_func=SGD, loss_func=nn.CrossEntropyLoss(), metrics=accuracy)
learn.fine_tune(10, 0.1)
| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.180775 | 0.170384 | 0.946488 | 00:11 |
| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.064815 | 0.054088 | 0.983512 | 00:11 |
| 1 | 0.067600 | 0.047392 | 0.984970 | 00:11 |
| 2 | 0.069272 | 0.052175 | 0.983065 | 00:10 |
| 3 | 0.080398 | 0.060341 | 0.980387 | 00:11 |
| 4 | 0.042787 | 0.045250 | 0.985030 | 00:11 |
| 5 | 0.031226 | 0.030384 | 0.990595 | 00:10 |
| 6 | 0.019606 | 0.019908 | 0.995238 | 00:11 |
| 7 | 0.015953 | 0.016687 | 0.996548 | 00:10 |
| 8 | 0.016785 | 0.015338 | 0.997470 | 00:11 |
| 9 | 0.016400 | 0.015170 | 0.997470 | 00:11 |
Looks great! We are actually predicting the full set of digits with almost perfect accuracy! Now that we understand the inner workings of neural networks, we can focus on more advanced approaches in the upcoming lessons.
References:
- Deng, L. (2012). The mnist database of handwritten digit images for machine learning research. IEEE Signal Processing Magazine, 29(6), 141–142.
- Zeiler, M. D., & Fergus, R. (2014). Visualizing and Understanding Convolutional Networks. ECCV.
- Howard, J., & Gugger, S. (2020). Deep Learning for Coders with fastai and PyTorch. O’Reilly Media.